Gaussian processes¶
Gaussian processes model a probability distribution over functions.
Let be some function mapping vectors to vectors. Then we can write:
where represents the mean vector:
and is the kernel function.
Kernel function¶
The kernel is a function that represents the covariance function for the Gaussian process.
The kernel can be thought of as a prior for the shape of the function, encoding our expectations for the amount of smoothness or non-linearity.
Not all conceivable kernels are valid. The kernel must produce covariance matrices that are positive-definite.
Gaussian kernel¶
Also known as the radial basis function or RBF kernel.
Some functions sampled from a GP with a Gaussian kernel:
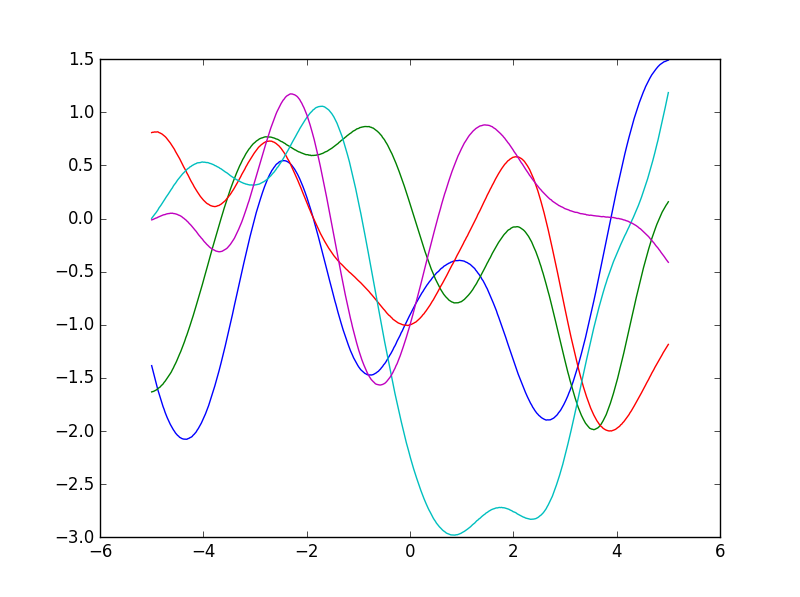
Sampling from a Gaussian process¶
The method is as follows:
- Decide on a vector of inputs
for which we want to compute
, where
is some function which we will sample from the Gaussian process.
- Compute the matrix
where
.
- Perform Cholesky decomposition on
, yielding a lower triangular matrix
.
- Sample a vector of numbers from a standard Gaussian distribution,
.
- Take the dot product of
and the vector
to get the samples
.