Loss functions¶
For classification problems, is equal to 1 if the example is a positive and 0 if it is a negative.
can take on any value (although predicting outside of the (0,1) interval is unlikely to be useful).
Classification¶
Cross-entropy loss¶
Loss function for classification.
where c are the classes. equals 1 if example
is in class
and 0 otherwise.
is the predicted probability that example
is in class
.
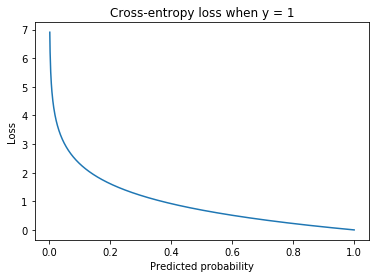
For discrete distributions (ie classification problems rather than regression) this is the same as the negative log-likelihood loss.
Hinge loss¶
Let positives be encoded as and negatives as
. Then the hinge loss is defined as:
The margin is a hyperparameter that is commonly set to 1.
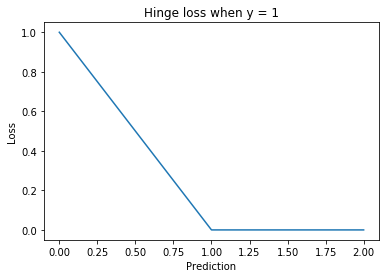
Used for training SVMs.
Focal loss¶
Variant of the cross-entropy loss, designed for use on datasets with severe class imbalance. It is defined as:
Where is a hyperparameter that determines the relative importance of the classes. If
the focal loss is equivalent to the cross-entropy loss.
Noise Contrastive Estimation¶
Like negative sampling, this is a technique for efficient learning when the number of output classes is large. Useful for language modelling.
A binary classification task is created to disambiguate pairs that are expected to be close to each other from ‘noisy’ examples put together at random.
In essence, rather than estimating , NCE estimates
where
if
has been sampled from the real distribution and
if
has been sampled from the noise distribution.
NCE makes training time at the output layer independent of the number of classes. It remains linear in time at evaluation, however.
is a hyperparameter, denoting the number of noise samples for each real sample.
is a label sampled from the data distribution and
is one sampled from the noise distribution.
if the pair
was drawn from the data distribution and 0 otherwise.
Embeddings¶
Contrastive loss¶
Loss function for learning embeddings, often used in face verification.
The inputs are pairs of examples and
where
if the two examples are of the similar and
if not.
Where and
are the embeddings for the two examples and
is a hyperparameter called the margin.
is a distance function, usually the Euclidean distance.
Intuition¶
If the two examples
and
are similar and we want to minimize the distance
. Otherwise (
) we wish to maximize it.
The margin¶
If we want to make
as large as possible to minimize the loss. However, beyond the threshold for classifying the example as a negative increasing this distance will not have any effect on the accuracy. The margin ensures this intuition is reflected in the loss function. Using the margin means increasing
beyond
has no effect.
There is no margin for when . This case is naturally bounded by 0 as the Euclidean distance cannot be negative.
Negative sampling¶
The problem is reframed as a binary classification problem.
where and
are two examples,
is the learned embedding function and
if the pair
are expected to be similar and
otherwise. The dot product measures the distance between the two embeddings.
Noise Contrastive Estimation¶
A binary classification task is created to disambiguate pairs that are expected to be close to each other from ‘noisy’ examples put together at random.
where and
are two examples,
is the learned embedding function and
if the pair
are expected to be similar and
if not (because they have been sampled from the noise distribution). The dot product measures the distance between the two embeddings and the sigmoid function transforms it to be between 0 and 1 so it can be interpreted as a prediction for a binary classifier.
This means maximising the probability that actual samples are in the dataset and that noise samples aren’t in the dataset. Parameter update complexity is linear in the size of the vocabulary. The model is improved by having more noise than training samples, with around 15 times more being optimal.
Triplet loss¶
Used for training embeddings with triplet networks. A triplet is composed of an anchor (), a positive example (
) and a negative example (
). The positive examples are similar to the anchor and the negative examples are dissimilar.
Where is a hyperparameter called the margin.
is a distance function, usually the the Euclidean distance.
The margin¶
We want to minimize and maximize
. The former is lower-bounded by 0 but the latter has no upper bound (distances can be arbitrarily large). However, beyond the threshold to classify a pair as a negative, increasing this distance will not help improve the accuracy, a fact which needs to be reflected in the loss function. The margin does this by ensuring that there is no gain from increasing
beyond
since the loss will be set to 0 by the maximum.
Regression¶
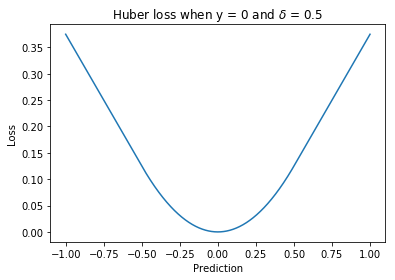
Huber loss¶
A loss function used for regression. It is less sensitive to outliers than the squared loss since there is only a linear relationship between the size of the error and the loss beyond .
Where is a hyperparameter.
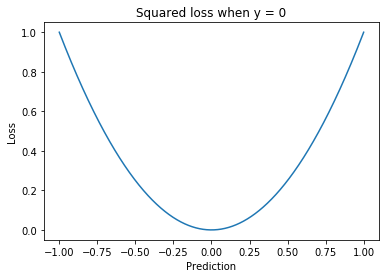
Squared loss¶
A loss function used for regression.
Disadvantages¶
The squaring means this loss function weights large errors more than smaller ones, relative to the magnitude of the error. This can be particularly harmful in the case of outliers. One solution is to use the Huber loss.